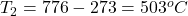A Jaguar XK8 convertible has an eight-cylinder engine. At the beginning of its compression stroke, one of the cylinders contains 499 cm3cm3

Question

A Jaguar XK8 convertible has an eight-cylinder engine. At the beginning of its compression stroke, one of the cylinders contains 499 cm3cm3 of air at atmospheric pressure (1.01×1051.01×105 PaPa) and a temperature of 27.0∘C∘C. At the end of the stroke, the air has been compressed to a volume of 46.2 cm3cm3 and the gauge pressure has increased to 2.72×1062.72×106 PaPa.

in progress 0
Thành Đạt 3 years 2021-08-17T06:58:22+00:00 1 Answers 329 views 0

Answers ( )

  1. nguyetanh
    1
    2021-08-17T07:00:11+00:00
    Reply

    Complete Question

    A Jaguar XK8 convertible has an eight-cylinder engine. At the beginning of its compression stroke, one of the cylinders contains 499cm3 of air at atmospheric pressure (1.01×105Pa) and a temperature of 27.0∘C. At the end of the stroke, the air has been compressed to a volume of 46.2cm3 and the gauge pressure has increased to 2.72×106Pa. Compute the final temperature.

    Answer:  

    The final temperature is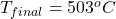 T_{final} = 503^o C

    Explanation:

    From the question we are given

           The volume of one of the cylinders is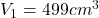 V_1 = 499cm^3

          The atmospheric pressure is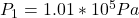 P_{1} = 1.01 *10^5Pa

           The temperature is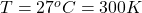 T = 27^oC = 300K

           Volume at the end of the stroke is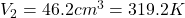 V_2 = 46.2cm^3 = 319.2 K

           The increased pressure  is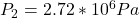 P_2 = 2.72 * 10^6Pa

    Now to obtain the temperature we are going to apply the ideal gas equation to this question and this is mathematically given as

                            PV = nRT

    Where P is the pressure , V sis the volume T is the temperature

    While is the rate constant and n is the number of mole which is constant in this question  hence

                           => \frac{PV}{T} = constant

                         => \frac{P_1V_1}{T_1} = \frac{P_2V_2}{T_2}

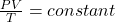
    Making T_2 the subject of the formula we have

                      => T_2 = T_1 (\frac{P_2}{P_1} ) (\frac{V_2}{V_1} )

                     => \ \ \ \ \ \ \ \ T_2 = 300(\frac{2.8*10^6Pa}{1.01*10^5Pa} )(\frac{46.2cm^3}{499cm^3} )

                                           = 776K

     Therefore  T_2 = 776-273 = 503^oC

                         

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )