Share
Two solenoids have the same cross-sectional area and length, but the first one has twice as many turns er unit length as the second. <
Question
Two solenoids have the same cross-sectional area and length, but the first one has twice as many turns er unit length as the second.
The ratio of the self-inductance of the second solenoid to that of the first is :
a. 1:2
b. 1:4
c. 2:1
d. 4:1
e. 1:1
in progress
0
Physics
4 years
2021-08-16T02:02:21+00:00
2021-08-16T02:02:21+00:00 2 Answers
31 views
0

Answers ( )
Answer:
option (b)
Explanation:
number of turns in the first solenoid, N1 = N
number of turns in the second solenoid, N2 = 2N
Let the current is i and the length is l and the area of crossection of the solenoid is A.
The formula for the self inductance of the solenoid is
It means the self inductance of the solenoid is directly proportional to the square of number of turns.
So,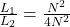
L1 : L2 = 1 : 4
Answer:
b:1:4
Explanation:
We are given that two solenoid.
Suppose ,the length of each solenoid=l
Cross-sectional area of each solenoid=A
Let , number of turns in in second solenoid,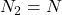
Number of turns in first solenoid,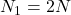
We have to find the ratio of self-inductance of the second solenoid to that of the first.
Self- inductance,L=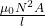
Using the formula
Self- inductance of one solenoid,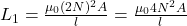
Self-inductance of second solenoid,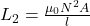
Hence, option b is true.