Spherical mirrors. Object O stands on the central axis of a spherical mirror. For this situation object distance is ps = +16 cm, the type of

Question

Spherical mirrors. Object O stands on the central axis of a spherical mirror. For this situation object distance is ps = +16 cm, the type of mirror is concave, and then the distance between the focal point and the mirror is 11 cm (without proper sign).

Find :

(a) the radius of curvature r (including sign),

(b) the image distance i, and

(c) the lateral magnification m. Also, determine whether the image is

(d) real or virtual ,

(e) inverted from object O or non inverted , and

(f) on the same side of the mirror as O or on the opposite side.

in progress 0
Bình An 4 years 2021-08-15T20:44:51+00:00 1 Answers 34 views 0

Answers ( )

  1. RobertKer
    0
    2021-08-15T20:46:08+00:00
    Reply

    Answer:

    a

    The radius of curvature is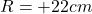 R= +22cm

    b

    the image distance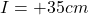 I= +35cm

    c

    the lateral magnification is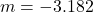 m = -3.182

    d

    The image is real given that the object distance is greater than the focal length and this is a type of setup that gives a real image in concave mirror

    e

    This would be inverted because from above we see that the image is real and all real image are inverted i concave mirror

    f

    This image would be on the same side of the object this is because both the image distance and the object distance are positive

    Explanation:

    From the question we are told that

                     The object distance is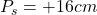 P_s = +16cm  

                      The focal length is  F_c = 11cm

    The focal length is mathematically given as

                         F_c = \frac{R}{2}

       Where R is the radius of curvature

    Now making R the subject of the formula above

                 R = 2F_c

                     = 2 *11 = +22cm (the positive sign is because it is in the real world size)

    The mathematical representation of the mirror formula is

                      \frac{1}{I} + \frac{1}{u} + \frac{1}{F_c}

                    \frac{1}{I} + \frac{1}{16} = \frac{1}{11}

                   \frac{1}{I} = \frac{1}{11} - \frac{1}{16}

                   \frac{1}{I} = \frac{5}{176}

                     = \frac{176}{5}

                     I = +35.2 cm

    Mathematically  lateral magnification is represented as

                 m = \frac{I}{u}

    Where I is the image distance and u is the object distance

          m= -\frac{35}{16} = -3.182      

                               

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )