By means of a rope whose mass is negligible, two blocks are suspended over a pulley, as the drawing shows, with m1 = 12.1 kg and m2 = 43.7 k

Question

By means of a rope whose mass is negligible, two blocks are suspended over a pulley, as the drawing shows, with m1 = 12.1 kg and m2 = 43.7 kg. The pulley can be treated as a uniform, solid, cylindrical disk. The downward acceleration of the 43.7 kg block is observed to be exactly one-half the acceleration due to gravity. Noting that the tension in the rope is not the same on each side of the pulley, find the mass of the pulley.

in progress 0
Dulcie 4 years 2021-08-13T17:18:54+00:00 1 Answers 12 views 0

Answers ( )

  1. Nho
    0
    2021-08-13T17:20:29+00:00
    Reply

    Answer:

    14.8 kg

    Explanation:

    We are given that

    m_1=43.7 kg

    m_2=12.1 kg

    g=9.8 m/s^2

    a=\frac{1}{2}(9.8)=4.9 m/s^2

    We have to find the mass of the pulley.

    According to question

    T_2-m_2 g=m_2 a

    T_2=m_2a+m_2g=m_2(a+g)=12.1(9.8+4.9)=177.87 N

    T_1=m_1(g-a)=43.7(9.8-4.9)=214.13 N

    Moment of inertia of pulley=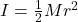I=\frac{1}{2}Mr^2

    (T_2-T_1)r=I(-\alpha)=\frac{1}{2}Mr^2(\frac{-a}{r})=\frac{1}{2}Mr(-4.9)

    Where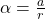 \alpha=\frac{a}{r}

    (177.87-214.13)=-\frac{1}{2}(4.9)M

    -36.26=-\frac{1}{2}(4.9)M

    M=\frac{36.26\times 2}{4.9}=14.8 kg

    Hence, the mass of the pulley=14.8 kg

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )