You’ve made the finals of the Science Olympics! As one of your tasks, you’re given 1.0 gg of aluminum and asked to make a wire, using all th

Question

You’ve made the finals of the Science Olympics! As one of your tasks, you’re given 1.0 gg of aluminum and asked to make a wire, using all the aluminum, that will dissipate 6.5 WW when connected to a 2.5 VV battery.

a)- What diameter will you choose for your wire?

b)-What length will you choose for your wire?

in progress 0
Vodka 4 years 2021-08-12T10:29:14+00:00 2 Answers 76 views 0

Answers ( )

  1. danthu
    0
    2021-08-12T10:30:24+00:00
    Reply

    Answer:

    a

    The diameter is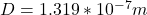 D =1.319*10^{-7} m

    b

    The length to choose is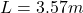 L= 3.57m

    Explanation:

       From the question we are told that

                The mass of aluminum is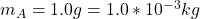  m_A = 1.0g = 1.0*10^{-3}kg

                 The expected power to dissipate is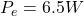 P_e = 6.5W

                  The potential difference is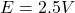  E = 2.5V

    First we need to obtain the resistance R which is mathematically  represented as

                          R = \frac{E^2}{P_e}

      Substituting values

                       R = \frac{2.5^2 }{6.5}

                          = 0.962 \ \Omega

    Next we obtain the volume of the aluminium which is mathematically represented as

                         v =\frac{m_A}{\rho_A}

    The value of the density of aluminium is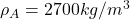  \rho_A=2700 kg/m^3

    Now substituting the value

                       v = \frac{1.0*10^{-3}}{2700}

                          = 0.37 *10^{-6}m^3

    The resistance can also be mathematically represented as

                      R = \frac{\rho L}{A}

      Where L is the length , A is the area  and \rho is resistivity

     and for aluminum the resistivity is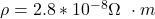 \rho = 2.8*10^{-8} \Omega \ \cdot m

    Now multiplying the denominator and the numerator by L i.e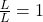 \frac{L}{L} = 1

                  R = \frac{\rho L}{A} [\frac{L}{L} ]

                      = \frac{\rho L ^2}{AL}

    But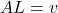  AL = v  i.e area × length = volume

                     R = \frac{\rho L ^2}{v}

    Now making L the subject of the formula in the question above

                      L = \sqrt{\frac{Rv}{\rho} }

                         = \sqrt{\frac{(0.962)(0.37*10^{-6})}{2.8*10{-8} } }

                        =3.57m

    Volume can also be mathematically represented as

                      v =AL

    Now making A the subject

                     A = \frac{v}{L}

                        = \frac{0.37 *10 ^{-6}}{3.57}

                       =1.036*10^{-7}m^2

    The area A is mathematically represented as

                     A = \pi r^2

    And  r = \frac{D}{2}

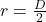
    Now substituting this into the formula for area

                    A= \pi \frac{D^2}{4}

      Making D(diameter)  the subject of the formula

                    D = \sqrt{\frac{4A}{\pi} }

                      =\sqrt{\frac{4 * 1.036 *10^{-7}}{3.142} }

                      =1.319*10^{-7}m

     

  2. minhkhang
    0
    2021-08-12T10:30:44+00:00
    Reply

    Answer:

    a) Diameter = 8.09 × 10⁻⁴m

    b) length = 2.26m

    Explanation:

    The relation between density, mass and volume is

    V = \frac{m}{p}

    v = \frac{1 \times 10^-^3kg }{2700kg/m^3} \\\\= 0.37 \times 10^-^6m^3

    The relation between power, resistance and voltage is ,

    R = \frac{V^2}{P}

    R = \frac{2.5}{6.5} \\\\= 0.385

    R = 0.385Ω

    The resistance of wire depend on the resistivity , area, and length of the wire as

    R = \frac{pL}{A}

    R = \frac{(pL)}{(A) }\frac{(L)}{(L)} \\\\R = \frac{pL^2}{AL} \\\\R = \frac{pL^2}{v}

    rearrange above equation for L

    L^2 = \frac{Rv}{p} \\\\L = \sqrt{\frac{Rv}{p} }

    L = \sqrt{\frac{0.385 \times 0.37 \times 10^-^6 }{2.8 \times 10^-^8} } \\\\L= 2.26m

    The volume of the aluminium wire is

    A = πr²

    A = \pi (\frac{D}{2} )^2\\\\A = \frac{\pi D }{4}

    D = \sqrt{\frac{4v}{L \pi } } \\\\D = \sqrt{\frac{4(0.37 \times 10^-^6}{2.26} } \\\\D = 8.09 \times 10^-^4m

    Diameter = 8.09 × 10⁻⁴m

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )