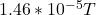One long wire lies along an x axis and carries a current of 43 A in the positive x direction. A second long wire is perpendicular to the xy

Question

One long wire lies along an x axis and carries a current of 43 A in the positive x direction. A second long wire is perpendicular to the xy plane, passes through the point (0, 5.1 m, 0), and carries a current of 72 A in the positive z direction. What is the magnitude of the resulting magnetic field at the point (0, 0.60 m, 0)

in progress 0
Khoii Minh 4 years 2021-08-09T12:28:54+00:00 1 Answers 10 views 0

Answers ( )

  1. nguyetanh
    0
    2021-08-09T12:30:30+00:00
    Reply

    Answer:

    1.46*10^{-5}T

    Explanation:

    Using the magnetic field equation:

    B = \frac {\mu_oI} {2p r}

    where:

    \mu_o = permeability of free space = 4p*10^{-7}T*m/A

    I = current in the wire

    r = distance from the wire to the point

    Magnetic field due to the wire on the x- axis can be calculated as:

    B = \frac {\mu_oI} {2p r}

    B= \frac{4p*10^{-7}*43}{2p*0.60}

    B = 1.43 *10^{-5} T

    Magnetic field due to the positive z-direction wire:

    B = \frac{\mu_ol}{2pr}

    B = \frac{4p*10^{-7}*72}{2p*5.1}

    B = 2.82 *10^{-6}T

    Now; adding these two vector components together to get the magnitude of the resultant vector; we have:

    = \sqrt{(1.43 *10^{-5})^2+(2.82 *10^{-6})^2}

    = 1.46*10^{-5}T

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )