The potential difference V(t) between the parallel plates of a capacitor is instantaneously increasing at a rate of 107 V/s. What is the dis

Question

The potential difference V(t) between the parallel plates of a capacitor is instantaneously increasing at a rate of 107 V/s. What is the displacement current (in mA) between the plates if the separation of the plates is 1.30 cm and they have an area of 0.174 m2

in progress 0
Khoii Minh 4 years 2021-08-06T20:22:54+00:00 1 Answers 20 views 0

Answers ( )

  1. Eirian
    0
    2021-08-06T20:24:43+00:00
    Reply

    Answer:

    The displacement current between the plates is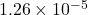 1.26 \times 10^{-5} mA

    Explanation:

    Given :

    Potential difference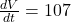 \frac{dV}{dt} = 107 \frac{V}{s}

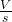
    Separation between plates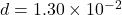 d = 1.30 \times 10^{-2} m

    Area of plates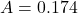 A = 0.174 m^{2}

    From the formula of displacement current,

       I_{d} = \epsilon _{o} A\frac{dE}{dt}

    We know that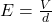 E = \frac{V}{d}.

    So we can modify above formula,

       I_{d} =( \frac{\epsilon _{o} A }{d} ) \frac{dV}{dt}

    Put the values in above equation,

       I_{d} = ( \frac{8.85 \times 10^{-12} \times 0.174 }{1.30 \times 10^{-2} } ) \times 107

       I_{d} = 1.26 \times 10^{-5} mA

    Therefore, the displacement current between the plates is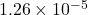 1.26 \times 10^{-5} mA

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )