A flat, square coil of 18 turns that has sides of length 14.0 cm is rotating in a magnetic field of strength 0.040 T. If the maximum emf pro

Question

A flat, square coil of 18 turns that has sides of length 14.0 cm is rotating in a magnetic field of strength 0.040 T. If the maximum emf produced in the coil is 36.0 mV, what is the angular velocity of the coil (in rad/s)? (Enter the magnitude.)

in progress 0
Tài Đức 4 years 2021-08-05T09:15:00+00:00 1 Answers 18 views 0

Answers ( )

  1. Helga
    0
    2021-08-05T09:16:35+00:00
    Reply

    Answer:

    The angular velocity of the coil is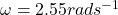 \omega =2.55 rad s^{-1}.

    Explanation:

    The expression  for the maximum emf is as follows;

    \epsilon =NBA\omega                                                    ……… (1)

    Here, \epsilon is the emf, {tex]\omega[/tex] is the angular velocity, N is the number of turns, B is the magnetic field and A is the area.

    Calculate the area of the square coil.

    Convert side of the length form cm to m.

    s=\frac{14}{100}m

    s= 0.14 m

    A=s^{2}

    Here, A is the area and s is the length of the side of the square.

    Put s= 0.14 m.

    A=0.0196 m^{2}

    Convert maximum emf from mV to V.

    \epsilon =36\times 10^{-3} V

    Calculate the angular velocity of the coil by rearranging the equation (1).

    \omega =\frac{\epsilon }{NBA}

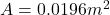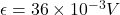    Put A=0.0196 m^{2}, \epsilon =36\times 10^{-3} V, B= 0.040 T and N= 18 turns.

    \omega =\frac{36\times 10^{-3} }{18(0.040)(0.0196)}

    \omega =2.55 rad s^{-1}

    Therefore, the angular velocity of the coil is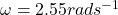 \omega =2.55 rad s^{-1}.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )