A long, hollow wire with inner radius a and outer radius b carries a uniform current density J. What is the magnetic field as a function of

Question

A long, hollow wire with inner radius a and outer radius b carries a uniform current density J. What is the magnetic field as a function of r, the distance from the center of the wire within the wire’s material (i.e. what is B(r) in the region a < r < b)?

in progress 0
Philomena 4 years 2021-08-05T02:39:37+00:00 1 Answers 71 views 0

Answers ( )

  1. Maris
    0
    2021-08-05T02:40:45+00:00
    Reply

    Answer:

    The magnetic field in the region a < r < b is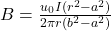 B=\frac{u_{0}I(r^{2}-a^{2}) }{2\pi r(b^{2}-a^{2}) }

    Explanation:

    If we have the a < r < b. The formula of current is:

    J=\frac{I_{total} }{A}

    Where:

    A = area enclosed by the loop.

    Itotal = total current in loop.

    J=\frac{I}{\pi b^{2}-\pi a^{2} }

    I_{enclosed} =JA_{enclosed}

    I_{enclosed} =\frac{I(\pi r^{2}- \pi a^{2})}{\pi b^{2}-\pi a^{2} }

    If we have the Ampere`s law:

    \int\limits^a_b {B} \, ds =u_{0} I_{enclosed} \\2B\pi r=u_{0} (\frac{I(\pi r^{2}-\pi ^{2} }{\pi ^{2}-\pi a^{2} } )\\B=\frac{u_{0}I(r^{2}-a^{2}) }{2\pi r(b^{2}-a^{2}) }

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )