Share
A uniform cylindrical grinding wheel of mass 50.0 kg and diameter 1.0 m is turned on by an electric motor. The friction in the bearings is n
Question
A uniform cylindrical grinding wheel of mass 50.0 kg and diameter 1.0 m is turned on by an electric motor. The friction in the bearings is negligible. What torque must be applied to the wheel to bring it from rest to 120 rev/min in 20 revolutions?
in progress
0
Physics
4 years
2021-08-04T23:23:12+00:00
2021-08-04T23:23:12+00:00 1 Answers
21 views
0

Answers ( )
Answer:
The torque must be applied to the wheel is 15.7 N-m.
Explanation:
Given that,
Mass of the wheel of cylinder, m = 50 kg
Diameter of the wheel, d = 1 m
Radius, r = 0.5 m
Initial speed off the wheel is 0
Final angular speed of the wheel, 120 rev/min = 12.56 rad/s
Angular displacement,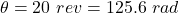
The torque is given by :
So, the torque must be applied to the wheel is 15.7 N-m.