A man walks along a straight path at a speed of 4 ft/s. A searchlight is located on the ground 6 ft from the path and is kept focused on the

Question

A man walks along a straight path at a speed of 4 ft/s. A searchlight is located on the ground 6 ft from the path and is kept focused on the man. At what rate is the searchlight rotating when the man is 8 ft from the point on the path closest to the searchlight

in progress 0
Ngọc Diệp 4 years 2021-08-03T07:53:13+00:00 1 Answers 16 views 0

Answers ( )

  1. Eirian
    0
    2021-08-03T07:54:22+00:00
    Reply

    We are given that,

    \frac{dx}{dt} = 4ft/s

    We need to find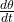 \frac{d\theta}{dt} when x=8ft

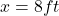
    The equation that relates x and \theta can be written as,

    \frac{x}{6} tan\theta

    x = 6tan\theta

    Differentiating each side with respect to t, we get,

    \frac{dx}{dt} = \frac{dx}{d\theta} \cdot \frac{d\theta}{dt}

    \frac{dx}{dt} = (6sec^2\theta)\cdot \frac{d\theta}{dt}

    \frac{d\theta}{dt} = \frac{1}{6sec^2\theta} \cdot \frac{dx}{dt}

    Replacing the value of the velocity

    \frac{d\theta}{dt} = \frac{1}{6} cos^2\theta (4)^2

    \frac{d\theta}{dt} = \frac{8}{3} cos^2\theta

    The value of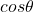 cos \theta could be found if we know the length of the beam. With this value the equation can be approximated to the relationship between the sides of the triangle that is being formed in order to obtain the numerical value. If this relation is known for the value of x = 6ft, the mathematical relation is obtained. I will add a numerical example (although the answer would end in the previous point) If the length of the beam was 10, then we would have to

    cos\theta = \frac{6}{10}

    \frac{d\theta}{dt} = \frac{8}{3} (\frac{6}{10})^2

    \frac{d\theta}{dt} = \frac{24}{25}

    Search light is rotating at a rate of 0.96rad/s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )