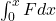The force exerted by a rubber band is given approximately by F=F0[L0−xL0−L20(L0+x)2]F=F0[L0−xL0−L02(L0+x)2] where L0L0 is the unstretched le

Question

The force exerted by a rubber band is given approximately by F=F0[L0−xL0−L20(L0+x)2]F=F0[L0−xL0−L02(L0+x)2] where L0L0 is the unstretched length, xx is the stretch, and F0F0 is a constant.Find the work needed tostretch the rubber band the distance, x.

in progress 0
Kiệt Gia 4 years 2021-08-02T20:06:25+00:00 1 Answers 55 views 0

Answers ( )

  1. quangkhai
    0
    2021-08-02T20:08:13+00:00
    Reply

    Answer:

    F_0(x+\frac{1}{2L_0}x^2+\frac{L^2_0}{L_0+x}-L_0)

    Explanation:

    We are given that

    Force exerted by a rubber band is given approximately by

    F=F_0(\frac{L_0+x}{L_0}-\frac{L^2_0}{(L_0+x)^2})

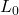    Where L_0=Unstretched  length

    x=Stretch length

    F_0=Constant

    We have to find the work needed to stretch the rubber band the distance x.

    Work done=\int_{0}^{x}Fdx

    W=\int_{0}^{x}F_0(\frac{L_0+x}{L_0}-\frac{L^2_0}{(L_0+x)^2}dx

    W=\int_{0}^{x}(\frac{F_0}{L_0}(L_0+x)-\frac{L^2_0F_0}{(L_0+x)^2})dx

    W=\frac{F_0}{L_0}[L_0x+\frac{x^2}{2}]^{x}_{0}+F_0L^2_0[\frac{1}{L_0+x}]^{x}_{0}

    W=\frac{F_0}{L_0}(L_0x+\frac{x^2}{2})+L^2_0F_0(\frac{1}{L_0+x}-\frac{1}{L_0})

    W=F_0(x+\frac{1}{2L_0}x^2+\frac{L^2_0}{L_0+x}-L_0)

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )