A thin film of cooking oil ( n = 1.47 ) is spread on a puddle of water ( n = 1.35 ) . What is the minimum thickness D min of the oil that wi

Question

A thin film of cooking oil ( n = 1.47 ) is spread on a puddle of water ( n = 1.35 ) . What is the minimum thickness D min of the oil that will strongly reflect blue light having a wavelength in air of 456 nm, at normal incidence?

in progress 0
Thu Nguyệt 4 years 2021-07-29T06:30:58+00:00 1 Answers 62 views 0

Answers ( )

  1. minhkhoi
    0
    2021-07-29T06:32:36+00:00
    Reply

    Answer:

    The minimum thickness of the oil is 77.55 nm

    Explanation:

    Given:

    Refractive index of oil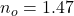 n_{o} = 1.47

    Refractive index of water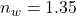 n_{w} = 1.35

    Wavelength of light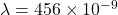 \lambda= 456 \times 10^{-9} m

    From the equation of thin film interference,

    The minimum thickness is given by,

        2n_{o} t = (n+\frac{1}{2}) \lambda

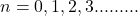    Where n = 0,1,2,3.........,t = thickness

    Here we have to find minimum thickness so we use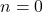 n = 0

         2n_{o} t =( 0+\frac{1}{2} )\lambda

       t = \frac{\lambda }{4 n_{o} }

       t = \frac{456 \times 10^{-9} }{4 \times 1.47}

       t = 77.55 \times 10^{-9} m

       t = 77.55 nm

    Therefore, the minimum thickness of the oil is 77.55 nm

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )