The pupil of the eye is the circular opening through which light enters. its diameter can vary from about 8.00 mm to about 2.00 mm to contro

Question

The pupil of the eye is the circular opening through which light enters. its diameter can vary from about 8.00 mm to about 2.00 mm to control the intensity of the light reaching the interior. calculate the angular resolution, θr, of the eye for light that has a wavelength of 558 nm in both bright light and dim light.

in progress 0
Ben Gia 4 years 2021-07-19T06:47:31+00:00 1 Answers 60 views 0

Answers ( )

  1. Dau
    0
    2021-07-19T06:49:04+00:00
    Reply

    Answer:

    The angular resolution is 0.0146°

    Explanation:

    Given:

    Diameter of pupil eye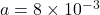 a = 8 \times 10^{-3} m

    Diameter of pupil eye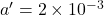 a' = 2 \times 10^{-3} m

    Wavelength of light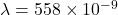 \lambda = 558 \times 10^{-9} m

    According to rayleigh criterion,

       \sin \theta = 1.22 \frac{\lambda}{a}

    Where \theta = angular resolution, a = diameter of aperture,

    For larger diameter a,

       \sin \theta _{1} = 1.22 \frac{558 \times 10^{-9} }{8 \times 10^{-3} }

       \theta _{1} = 0.0049°

    For smaller diameter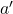 a',

        \sin \theta _{2} = 1.22 \frac{558 \times 10^{-9} }{2 \times 10^{-3} }

       \theta _{2} = 0.0195°

    For finding the angular resolution,

       \theta _{r} = \theta _{2} - \theta _{1}

       \theta _{r} = 0.0195 - 0.0049

       \theta _{r} = 0.0146°

    Therefore, the angular resolution is 0.0146°

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )