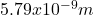Share
German physicist Werner Heisenberg related the uncertainty of an object’s position ( Δ x ) to the uncertainty in its velocity ( Δ v ) Δ x ≥
Question
German physicist Werner Heisenberg related the uncertainty of an object’s position ( Δ x ) to the uncertainty in its velocity ( Δ v ) Δ x ≥ h 4 π m Δ v where h is Planck’s constant and m is the mass of the object. The mass of an electron is 9.11 × 10 − 31 kg. What is the uncertainty in the position of an electron moving at 1.00 × 10 6 m/s with an uncertainty of Δ v = 0.01 × 10 6 m/s ?
in progress
0
Physics
4 years
2021-08-03T10:31:55+00:00
2021-08-03T10:31:55+00:00 1 Answers
16 views
0

Answers ( )
Answer:
The uncertainty in the position of the electron is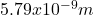
Explanation:
The Heisenberg uncertainty principle is defined as:
Where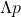 is the uncertainty in momentum,
is the uncertainty in momentum, 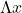 is the uncertainty in position and h is the Planck’s constant.
is the uncertainty in position and h is the Planck’s constant.
The momentum is defined as:
Therefore, equation 2 can be replaced in equation 1
Since, the mass of the electron is constant, v will be the one with an associated uncertainty.
Then,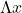 can be isolated from equation 3
can be isolated from equation 3
But
Hence, the uncertainty in the position of the electron is