A village maintains a large tank with an open top, containing water for emergencies. The water can drain from the tank through a hose of dia

Question

A village maintains a large tank with an open top, containing water for emergencies. The water can drain from the tank through a hose of diameter 6.60 cm. The hose ends with a nozzle of diameter 2.20 cm. A rubber stopper is inserted into the nozzle. The water level in the tank is kept 7.50 m above the nozzle. (a) Calculate the friction force exerted on the stopper by the nozzle. (b) The stopper is removed. What mass of water flows from the nozzle in 2.00 h

in progress 0
King 4 years 2021-08-02T05:15:39+00:00 1 Answers 13 views 0

Answers ( )

  1. mocmien2
    0
    2021-08-02T05:16:39+00:00
    Reply

    Answer:

    (A) Frictional force will be equal to 27.92 N

    (B) Mass is equal to 33120 kg

    Explanation:

    (A) Diameter of nozzle d = 2.20 cm

    So radius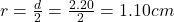 r=\frac{d}{2}=\frac{2.20}{2}=1.10cm

    eight h = 7.5 m

    Density of water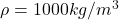 \rho =1000kg/m^3

    Acceleration due to gravity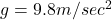 g=9.8m/sec^2

    Pressure on the rubber stopper

    P=\rho hg

    p=1000\times 7.5\times 9.8=73500Pa

    Area of cross section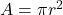 A=\pi r^2

    A=3.14\times 0.01^2=3.799\times 10^{-4}m^2

    So force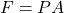 F=PA

    F=73500\times 3.799\times 10^{-4}=27.92N

    (B) Speed of the water through nozzle

    v=\sqrt{2gh}

    =\sqrt{2\times 9.8\times 7.5}=12.12m/sec

    Volume of water flow

    V=vA=12.12\times 3.799\times 10^{-4}=0.0046m^3/sec

    Mass of water flow per sec

    m=\rho V=1000\times 0.0046=4.6kg

    Total time t = 2 hour = 2×3600 = 7200 sec

    So total mass flow

    m=4.6\times 7200=33120kg

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )