Share
3. A certain wire, 3 m long, stretches by 1.2 mm when under tension of 200 N. By how much does an equally thick wire 6 m long, made of
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
The extension of the second wire is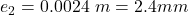
Explanation:
From the question we are told that
The length of the wire is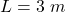
The elongation of the wire is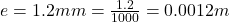
The tension is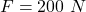
The length of the second wire is
Generally the Young’s modulus(Y) of this material is
Where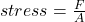
Where A is the area which is evaluated as
and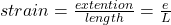
So
Since the wire are of the same material Young’s modulus(Y) is constant
So we have
Now the ration between the first and the second wire is
Since tension , radius are constant
We have
substituting values