Block 1, of mass m1 = 2.50 kg , moves along a frictionless air track with speed v1 = 27.0 m/s. It collides with block 2, of mass m2 = 33.0 k

Question

Block 1, of mass m1 = 2.50 kg , moves along a frictionless air track with speed v1 = 27.0 m/s. It collides with block 2, of mass m2 = 33.0 kg , which was initially at rest. The blocks stick together after the collision.A. Find the magnitude pi of the total initial momentum of the two-block system. Express your answer numerically.B. Find vf, the magnitude of the final velocity of the two-block system. Express your answer numerically.C. what is the change deltaK= Kfinal- K initial in the two block systems kinetic energy due to the collision ? Express your answer numerically in joules.

in progress 0
Lệ Thu 4 years 2021-09-01T12:08:18+00:00 1 Answers 7 views 0

Answers ( )

  1. Sigrid
    0
    2021-09-01T12:10:01+00:00
    Reply

    Answer:

    a

    The total initial momentum of the two-block system is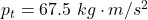  p_t = 67.5 \ kg \cdot m/s^2

    b

    The magnitude of the final velocity of the two-block system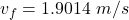 v_f = 1.9014 \ m/s

    c

     the change ΔK=Kfinal−Kinitial in the two-block system’s kinetic energy due to the collision is  

        \Delta KE =- 847.08 \ J

    Explanation:

    From the question we are told that

        The mass of first  block  is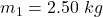 m_1 = 2.50 \ kg

          The initial velocity of first   block is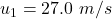 u_1 = 27.0 \ m/s

              The mass of second block is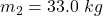  m_2 = 33.0\ kg

              initial velocity of second block is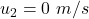  u_2 = 0 \ m/s

             

    The magnitude of the of the total initial momentum of the two-block system is mathematically repented as

            p_i = (m_1 * u_1 ) + (m_2 * u_2)

    substituting values

            p_i = (2.50* 27 ) + (33 * 0)

            p_t = 67.5 \ kg \cdot m/s^2

    According to the law of linear momentum conservation

            p_i = p_f

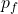    Where  p_f is the total final momentum of the system which is mathematically represented as

           p_f = (m_+m_2) * v_f

    Where v_f is the final velocity of the system

          p_i = (m_1 +m_2 ) v_f

    substituting values

           67.5 = (2.50+33 ) v_f

            v_f = 1.9014 \ m/s

    The change in kinetic energy is mathematically represented as

         \Delta KE = KE_f -KE_i

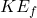    Where KE_f is the final kinetic energy of the two-body system  which is mathematically represented as

            KE_f = \frac{1}{2} (m_1 +m_2) * v_f^2

    substituting values

            KE_f = \frac{1}{2} (2.50 +33) * (1.9014)^2

            KE_f =64.17 J

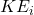    While KE_i is the initial kinetic energy of the two-body system

         KE_i = \frac{1}{2} * m_1 * u_1^2

    substituting values

           KE_i = \frac{1}{2} * 2.5 * 27^2

            KE_i = 911.25 \ J

    So

        \Delta KE = 64.17 -911.25

      \Delta KE =- 847.08 \ J

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )