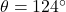Share
What is the sum of the following four vectors in (a) unit-vector notation, and as (b) a magnitude and (c) an angle? Positive angles are coun
Question
What is the sum of the following four vectors in (a) unit-vector notation, and as (b) a magnitude and (c) an angle? Positive angles are counterclockwise from the positive direction of the x axis; negative angles are clockwise. = 4.00 m, at 65.0° = 5.00 m, at -235°
in progress
0
Physics
4 years
2021-08-30T19:11:38+00:00
2021-08-30T19:11:38+00:00 1 Answers
7 views
0

Answers ( )
Answer:
The angle will be “124°“. The further explanation is given below.
Explanation:
As we know,
(a)…
Let the resultant of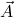 ,
, 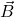 ,
, 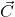 and
and  will be
will be 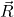 , then
, then
⇒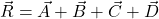
On putting values, we get
⇒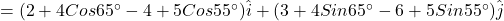
⇒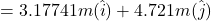
(b)…
On squaring both sides, we get
⇒
⇒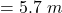
(c)…
Let the resultant angle will be “ “,
“,
⇒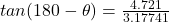
⇒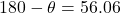
⇒