A hollow cylinder with an inner radius of 5 mm and an outer radius of 26 mm conducts a 4-A current flowing parallel to the axis of the cylin

Question

A hollow cylinder with an inner radius of 5 mm and an outer radius of 26 mm conducts a 4-A current flowing parallel to the axis of the cylinder. If the current density is uniform throughout the wire, what is the magnitude of the magnetic field at a point 12 mm from its center

in progress 0
Thạch Thảo 4 years 2021-08-29T00:45:34+00:00 1 Answers 16 views 0

Answers ( )

  1. lethu
    0
    2021-08-29T00:46:34+00:00
    Reply

    Answer:

    B = 38.2μT

    Explanation:

    By the Ampere’s law you have that the magnetic field generated by a current, in a wire, is given by:

    B=\frac{\mu_o I_r}{2\pi r}     (1)

    μo: magnetic permeability of vacuum = 4π*10^-7 T/A

    r: distance from the center of the cylinder, in which B is calculated

    Ir: current for the distance r

    In this case, you first calculate the current Ir, by using the following relation:

    I_r=JA_r

    J: current density

    Ar: cross sectional area for r in the hollow cylinder

    Ar is given by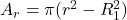  A_r=\pi(r^2-R_1^2)

    The current density is given by the total area and the total current:

    J=\frac{I_T}{A_T}=\frac{I_T}{\pi(R_2^2-R_1^2)}

    R2: outer radius = 26mm = 26*10^-3 m

    R1: inner radius = 5 mm = 5*10^-3 m

    IT: total current  = 4 A

    Then, the current in the wire for a distance r is:

    I_r=JA_r=\frac{I_T}{\pi(R_2^2-R_1^2)}\pi(r^2-R_1^2)\\\\I_r=I_T\frac{r^2-R_1^2}{R_2^2-R_1^2}  (2)

    You replace the last result of equation (2) into the equation (1):

    B=\frac{\mu_oI_T}{2\pi r}(\frac{r^2-R_1^2}{R_2^2-R_1^2})

    Finally. you replace the values of all parameters:

    B=\frac{(4\pi*10^{-7}T/A)(4A)}{2\PI (12*10^{-3}m)}(\frac{(12*10^{-3})^2-(5*10^{-3}m)^2}{(26*10^{-3}m)^2-(5*10^{-3}m)^2})\\\\B=3.82*10^{-5}T=38.2\mu T

    hence, the magnitude of the magnetic field at a point 12 mm from the center of the hollow cylinder, is 38.2μT

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )