Share
A block of mass M is suspended from a ceiling by a spring with spring stiffness constant k. A penny of mass m is placed on top of the block.
Question
A block of mass M is suspended from a ceiling by a spring with spring stiffness constant k. A penny of mass m is placed on top of the block. What is the maximum amplitude of oscillations that will allow the penny to just stay on top of the block
in progress
0
Physics
4 years
2021-08-26T06:30:28+00:00
2021-08-26T06:30:28+00:00 1 Answers
38 views
0

Answers ( )
Answer:
Explanation:
Given that:
Mass of block M
Mass of penny m
spring stiffness constant k
The frequency of oscillation of the block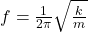
The angular velocity is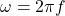
when the penny is resting on the block
The acceleration of the penny = acceleration of the block
If R is the reaction of the block on the penny
The penny will leave the block if R = 0
Therefore the amplitude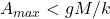 for the penny to remain on the block
for the penny to remain on the block