Share
A rotating wheel with diameter 0.800 m is speeding up with constant angular acceleration. The speed of a point on the rim of the wheel incre
Question
A rotating wheel with diameter 0.800 m is speeding up with constant angular acceleration. The speed of a point on the rim of the wheel increases from 3.00 m/s to 6.00 m/s while the wheel turns through 4.00 revolutions.
Required:
What is the angular acceleration of the wheel?
in progress
0
Physics
4 years
2021-08-21T14:58:05+00:00
2021-08-21T14:58:05+00:00 1 Answers
29 views
0

Answers ( )
Answer:
The angular acceleration of the wheel is 3.357rad/s²
Explanation:
Given;
Diameter of the wheel, d = 0.8 m
radius of the wheel, r = 0.4 m
initial velocity of the wheel, u = 3 m/s
final velocity of the wheel, v = 6 m/s
number of revolutions of the wheel, N = 4 rev.
Convert the linear velocity in m/s to angular velocity in rad/s;
v = ωr
ω = v / r
initial angular velocity,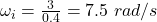
final angular velocity,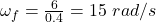
The angular acceleration of the wheel is calculated as;
where;
α is the angular acceleration (rad / s²)
θ is the angular rotation (rad)
θ = Number of revolutions x 2π rad/rev
= 4 rev. x 2π rad/rev
= 25.136 rad.
α = 3.357 rad/s²
Therefore, the angular acceleration of the wheel is 3.357rad/s²