Share
A centrifuge has an angular velocity of 3,000 rpm, what is the acceleration (in unit of the earth gravity) at a point with a radius of 10 cm
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
Explanation:
Let suppose that centrifuge is rotating at constant angular speed, which means that resultant acceleration is equal to radial acceleration at given radius, whose formula is:
Where:
The angular speed is first determined:
Where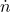 is the angular speed, measured in revolutions per minute.
is the angular speed, measured in revolutions per minute.
If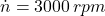 , the angular speed measured in radians per second is:
, the angular speed measured in radians per second is:
Now, if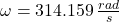 and
and 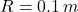 , the resultant acceleration is then:
, the resultant acceleration is then:
If gravitational acceleration is equal to 9.807 meters per square second, then the radial acceleration is equivalent to 1006.382 times the gravitational acceleration. That is: