If the set W is a vector space, find a set S of vectors that spans it. Otherwise, state that W is not a vector space. W is the set of all ve

Question

If the set W is a vector space, find a set S of vectors that spans it. Otherwise, state that W is not a vector space. W is the set of all vectors of the form [a – 4b 5 4a + b -a – b], where a and bare arbitrary real numbers.
a. [1 5 4 -1], [-4 0 1 -1]
b. [1 0 4 -1], [-4 5 1 -1]
c. [1 0 4 -1], [-4 0 1 -1], [0 5 0 0]
d. Not a vector space

in progress 0
MichaelMet 4 years 2021-08-16T05:03:34+00:00 1 Answers 123 views 0

Answers ( )

  1. thuthao
    0
    2021-08-16T05:05:26+00:00
    Reply

    Answer:

    Choice d. The set of vectors: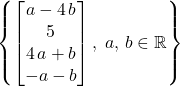 \displaystyle \left\{\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix},\; a,\, b\in \mathbb{R} \right\} isn’t a vector space over \mathbb{R}.

    Explanation:

    Let a set of vectors V to be a vector field over some field \mathbb{F} (for this question, that “field” is the set of all real number.) The following must be true:

    • The set of vectors V includes the identity element \mathbf{0}. In other words, there exists a vector \mathbf{0} \in V such that for all \mathbf{v} \in V, \mathbf{v} + \mathbf{0} = \mathbf{v}.
    • V should be closed under vector addition. In other words, for all \mathbf{u},\, \mathbf{v} \in V, \mathbf{u} + \mathbf{v} \in V.
    • V should also be closed under scalar multiplication. In other words, for all \mathbf{v} \in V and all “scalar” m \in \mathbb{F} (in this question, the “field” is the set of all real numbers, so m can be any real number,) a\,\mathbf{v} \in V.

    Note that in the general form of a vector in V, the second component is a always non-zero. Because of that non-zero component,

    Assume by contradiction that V is indeed a vector field. Therefore, it should contain a zero vector. Let \mathbf{0} denote that zero vector. For all \mathbf{v} \in V, \mathbf{v} + \mathbf{0} = \mathbf{v}.

    Using the definition of set 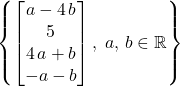V: \displaystyle \left\{\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix},\; a,\, b\in \mathbb{R} \right\}, there exist real numbers a and b, such that:

    \displaystyle \mathbf{v} = \begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix}.

    Hence, \mathbf{v} + \mathbf{0} = \mathbf{v} is equivalent to:

    \displaystyle \begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix} + \mathbf{0} = \begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix}.

    Apply the third property that V is closed under scalar multiplication. -1 is indeed a real number. Therefore, if \mathbf{v} is in

    Therefore:

    \displaystyle -\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix} \in V.

    Apply the second property and add \displaystyle - \mathbf{v} = -\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix} to both sides of \mathbf{v} + \mathbf{0} = \mathbf{v}. The left-hand side becomes:

    \mathbf{v} - \mathbf{v} + \mathbf{0} = \mathbf{0}.

    The right-hand side becomes:

    \displaystyle \begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix} -\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix} = \begin{bmatrix}a - 4\, b - (a - 4\, b) \\ 5 - 5 \\ 4\, a+ b-(4\, a+ b)\\ -a -b - (-a -b)\end{bmatrix} = \begin{bmatrix}0 \\ 0 \\ 0 \\0\end{bmatrix}.

    Therefore:

    \displaystyle \mathbf{0} = \begin{bmatrix}0 \\ 0 \\ 0 \\0\end{bmatrix}.

    However, \mathbf{0} = \displaystyle \begin{bmatrix}0 \\ 0 \\ 0 \\0\end{bmatrix} isn’t a member of the set \displaystyle V = \left\{\begin{bmatrix}a - 4\, b \\ 5 \\ 4\, a+ b\\ -a -b\end{bmatrix},\; a,\, b\in \mathbb{R} \right\}. That’s a contradiction, because \mathbf{0} was supposed to be part of V.

    Hence, V isn’t a vector space by contradiction.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )