a proton moves in a circle of radius 0.4 when it enters a region with a magnetic field of 1.0t which points into the plane the speed of the

Question

a proton moves in a circle of radius 0.4 when it enters a region with a magnetic field of 1.0t which points into the plane the speed of the proton is

in progress 0
Gerda 4 years 2021-08-12T07:11:04+00:00 1 Answers 7 views 0

Answers ( )

  1. ngockhue
    0
    2021-08-12T07:12:09+00:00
    Reply

    Answer:

    4 x 10⁷m/s

    Explanation:

    When a charged particle moves in a curved path in a magnetic field, it experiences some magnetic force, and in the absence of any other force, which supplies the centripetal force needed to keep the particle in balance.

    Let the magnetic force be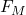 F_{M}

    Let the centripetal force be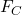 F_{C}

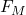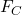    => F_{M} = F_{C}           ————–(i)

    We know that;

    F_{M} = qvBsinθ

    Where;

    q = charge on the particle

    v = speed of the particle

    B = magnetic field intensity

    θ = angle between the speed and magnetic field vectors

    Also;

    F_{C} = \frac{mv^2}{r}

    Where;

    m = mass of the particle

    v = velocity/speed of the particle

    r = radius of the circular path of motion.

    From equation (i)

    qvBsinθ =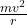 \frac{mv^2}{r}           [divide both sides by v]

    qBsinθ =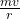 \frac{mv}{r}              [make v subject of the formula]

    v = qrBsinθ / m            ——————–(ii)

    From the question;

    B = 1.0T

    r = 0.4m

    θ = 90°     [since magnetic field is always perpendicular to velocity]

    q = 1.6 x 10⁻¹⁹C        [charge of a proton]

    m = 1.6 x 10⁻²⁷kg        [mass of a proton]

    Substitute these values into equation(ii) as follows;

    v = (1.6 x 10⁻¹⁹ x 0.4 x 1.0 x sin90°) /  (1.6 x 10⁻²⁷)

    v = 4 x 10⁷ m/s

    Therefore the speed of the proton is 4 x 10⁷m/s

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )