Share
The tires of a car make 77 revolutions as the car reduces its speed uniformly from 92.0 km/h to 60.0 km/h. The tires have a diameter of 0.84
Question
The tires of a car make 77 revolutions as the car reduces its speed uniformly from 92.0 km/h to 60.0 km/h. The tires have a diameter of 0.84 m.
1. What was the angular acceleration of the tires?
2. If the car continues to decelerate at this rate, how much more time is required for it to stop?
3. If the car continues to decelerate at this rate, how far does it go? Find the total distance.
in progress
0
Physics
4 years
2021-08-02T05:40:04+00:00
2021-08-02T05:40:04+00:00 1 Answers
18 views
0

Answers ( )
Answer:
the answer is below
Explanation:
1)
r=0.84/2=0.42
The initial velocity (u) = 92 km/h = 92 × 1000 / 3600 m/s = 25.56 m/s.
the initial angular velocity (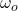 ) =
) = 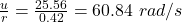
The final velocity (v) = 60 km/h = 60 × 1000 / 3600 m/s = 16.67 m/s.
the final angular velocity ( ) =
) = 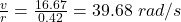
Using:
2)
Using:
3)