Share
A long straight conducting rod carries a current I with a non-uniform current density J = ar2, and has a radius R. The value of the constant
Question
A long straight conducting rod carries a current I with a non-uniform current density J = ar2, and has a radius R. The value of the constant is 28.5 A/mm4 and the radius of the rod is 5.20 mm. Determine the magnitude of the magnetic field at the following points.(a) r1 = R/2(b) r2 = 2R
in progress
0
Physics
4 years
2021-07-25T18:15:47+00:00
2021-07-25T18:15:47+00:00 1 Answers
32 views
0

Answers ( )
Answer:
Following are the solution to this question:
Explanation:
Given value:
Current density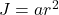
value of the constant is=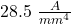
radius = 5.20 mm
magnetic permeability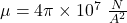
calculating the area element for the straight circular conduction rod
:
Calculating the current, which is carrying in rod
Calculating the above equation with the limit value that is 0 to r.
The calculated current value which is carried by the rod is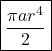
In option (a)
calculating the magnitude of the magnetic field at the point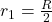
Substituting the above value: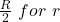
Thus, the magnitude of the magnetic field at the point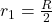 is
is 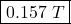
In option (b)
In this, we calculate the magnitude of the magnetic field at the point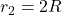
Substituting the values
Thus, the magnitude of the magnetic field at the point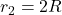 is
is