Share
How much energy would be required to move the earth into a circular orbit with a radius 2.0 kmkm larger than its current radius
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Answer:
Explanation:
G = Gravitational constant =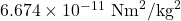
M = Mass of Sun =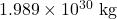
m = Mass of Earth =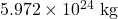
Energy required is given by
The energy required would be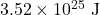 .
.