Share
Coherent light with wavelength of 580 nm passes through two very narrow slits, and the interference pattern is observed on a screen a distan
Question
Coherent light with wavelength of 580 nm passes through two very narrow slits, and the interference pattern is observed on a screen a distance of 3.00 m from the slits. The first-order bright fringe is at 4.81 mm from the center of the central bright fringe. For what wavelength of light will the first-order dark fringe be observed at this same point on the screen?
in progress
0
Physics
5 years
2021-09-01T01:08:38+00:00
2021-09-01T01:08:38+00:00 1 Answers
9 views
0

Answers ( )
Answer:
the required wavelength is 1.15815 μm
Explanation:
Given the data in the question;
The position of bright fringes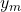 on screen in double slit experiment is expressed as follows;
on screen in double slit experiment is expressed as follows;
solving for d, we substitute 1 for m
y₁ = (1)λD / d
d = λD / y₁
given that λ = 580 nm = 5.8 × 10⁻⁷ m, D = 3.00 m and y₁= y₀ = 4.81 mm = 0.00481 m
so we substitute
d = λD / y₁
d = ( 5.8 × 10⁻⁷ m × 3.00 m ) / 0.00481 m
d = 0.00000174 m² / 0.00481 m
d = 3.6117 × 10⁻⁴ m
Now, position of dark fringe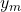 on screen in double slit experiment is expressed as;
on screen in double slit experiment is expressed as;
we substitute 0 for m
y₀ = ( 0 + 1/2 )λD / d
y₀ = λD / 2d
2y₀d = λD
λ = 2y₀d / D
we substitute
λ = ( 2(0.00481 m) ( 3.6117 × 10⁻⁴ m) ) / 3.0 m
λ = 1.15815 × 10⁻⁶ m
λ = 1.15815 μm
Therefore, the required wavelength is 1.15815 μm