A physics student of mass 43.0 kg is standing at the edge of the flat roof of a building, 12.0 m above the sidewalk. An unfriendly dog is ru

Question

A physics student of mass 43.0 kg is standing at the edge of the flat roof of a building, 12.0 m above the sidewalk. An unfriendly dog is running across the roof toward her. Next to her is a large wheel mounted on a horizontal axle at its center. The wheel, used to lift objects from the ground to the roof, has a light crank attached to it and a light rope wrapped around it; the free end of the rope hangs over the edge of the roof. The student radius 0.300 m and a moment of inertia of 9.60 kg m^2 for rotation about the axle, how long does it take her to reach the side walk, and how fast will she be moving just beofre she lands?

in progress 0
Ngọc Hoa 4 years 2021-09-01T00:40:23+00:00 1 Answers 122 views 0

Answers ( )

  1. yenoanh
    0
    2021-09-01T00:41:27+00:00
    Reply

    Answer:

    The speed of the student just before she lands, v₂ is approximately 8.225 m/s

    Explanation:

    The given parameters are;

    The mass of the physic student, m = 43.0 kg

    The height at which the student is standing, h = 12.0 m

    The radius of the wheel, r = 0.300 m

    The moment of inertia of the wheel, I = 9.60 kg·m²

    The initial potential energy of the female student, P.E.₁ = m·g·h₁

    Where;

    m = 43.0 kg

    g = The acceleration due to gravity ≈ 9.81 m/s²

    h = 12.0 h

    ∴ P.E.₁ = 43 kg × 9.81 m/s² × 12.0 m = 5061.96 J

    The kinetic rotational energy of the wheel and kinetic energy of the student supporting herself from the rope she grabs and steps off the roof, K₁, is given as follows;

    K_1 = \dfrac{1}{2} \cdot m \cdot v_{1}^2+\dfrac{1}{2} \cdot I \cdot \omega_{1}^2

    The initial kinetic energy, 1/2·m·v₁² and the initial kinetic rotational energy, 1/2·m·ω₁² are 0

    ∴ K₁ = 0 + 0 = 0

    The final potential energy of the student when lands. P.E.₂ = m·g·h₂ = 0

    Where;

    h₂ = 0 m

    The final kinetic energy, K₂, of the wheel and student is give as follows;

    K_2 = \dfrac{1}{2} \cdot m \cdot v_{2}^2+\dfrac{1}{2} \cdot I \cdot \omega_{2}^2

    Where;

    v₂ = The speed of the student just before she lands

    ω₂ = The angular velocity of the wheel just before she lands

    By the conservation of energy, we have;

    P.E.₁ + K₁ = P.E.₂ + K₂

    ∴ m·g·h₁ +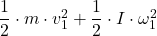 \dfrac{1}{2} \cdot m \cdot v_{1}^2+\dfrac{1}{2} \cdot I \cdot \omega_{1}^2 = m·g·h₂ +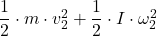 \dfrac{1}{2} \cdot m \cdot v_{2}^2+\dfrac{1}{2} \cdot I \cdot \omega_{2}^2

    Where;

    ω₂ = v₂/r

    ∴ 5061.96 J + 0 = 0 +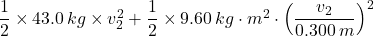 \dfrac{1}{2} \times 43.0 \, kg \times v_{2}^2+\dfrac{1}{2} \times 9.60 \, kg\cdot m^2 \cdot \left (\dfrac{v_2}{0.300 \, m} }\right ) ^2

    5,061.96 J = 21.5 kg × v₂² + 53.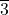\overline 3 kg × v₂² = 21.5 kg × v₂² + 160/3 kg × v₂²

    v₂² = 5,061.96 J/(21.5 kg + 160/3 kg) ≈ 67.643118 m²/s²

    v₂ ≈ √(67.643118 m²/s²) ≈ 8.22454363 m/s

    The speed of the student just before she lands, v₂ ≈ 8.225 m/s.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )