A solenoid that is 93.9 cm long has a cross-sectional area of 17.3 cm2. There are 1270 turns of wire carrying a current of 7.80 A. (a) Calcu

Question

A solenoid that is 93.9 cm long has a cross-sectional area of 17.3 cm2. There are 1270 turns of wire carrying a current of 7.80 A. (a) Calculate the energy density of the magnetic field inside the solenoid. (b) Find the total energy in joules stored in the magnetic field there (neglect end effects).

in progress 0
Thu Giang 3 years 2021-08-24T11:49:33+00:00 1 Answers 4 views 0

Answers ( )

  1. Vodka
    0
    2021-08-24T11:51:14+00:00
    Reply

    Answer:

    65.6\ \text{J/m}^3

    0.11\ \text{J}

    Explanation:

    B = Magnetic field =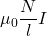 \mu_0 \dfrac{N}{l}I

    \mu_0 = Vacuum permeability = 4\pi10^{-7}\ \text{H/m}

    N = Number of turns = 1270

    l = Length of solenoid = 93.9 cm = 0.939 m

    I = Current = 7.8 A

    A = Area of solenoid =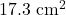 17.3\ \text{cm}^2

    Energy density of a solenoid is given by

    u_m=\dfrac{B^2}{2\mu_0}\\\Rightarrow u_m=\dfrac{(\mu_0 \dfrac{N}{l}I)^2}{2\mu_0}\\\Rightarrow u_m=\dfrac{\mu_0N^2I^2}{2l^2}\\\Rightarrow u_m=\dfrac{4\pi\times 10^{-7}\times 1230^2\times 7.8^2}{2\times 0.939^2}\\\Rightarrow u_m=65.6\ \text{J/m}^3

    The energy density of the magnetic field inside the solenoid is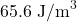 65.6\ \text{J/m}^3

    Energy is given by

    U_m=u_mAl\\\Rightarrow U_m=65.6\times 17.3\times 10^{-4}\times 0.939\\\Rightarrow U_m=0.11\ \text{J}

    The total energy in joules stored in the magnetic field is 0.11\ \text{J}.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )