Share
A 34-kg child runs with a speed of 2.8 m/s tangential to the rim of a stationary merrygo-round. The merry-go-round has a momentum of inertia
Question
A 34-kg child runs with a speed of 2.8 m/s tangential to the rim of a stationary merrygo-round. The merry-go-round has a momentum of inertia of 510 kg*m2 and a radius of 2.31 m. When the child jumps onto the merry-go-round, the entire system begins to rotate. What is the angular speed of the system
in progress
0
Physics
3 years
2021-08-16T03:48:25+00:00
2021-08-16T03:48:25+00:00 1 Answers
48 views
0

Answers ( )
Answer: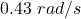
Explanation:
Given
Mass of child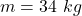
speed of child is
Moment of inertia of merry go round is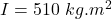
radius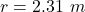
Conserving the angular momentum