What would the radius (in mm) of the Earth have to be in order for the escape speed of the Earth to equal (1/21) times the speed of light (3

Question

What would the radius (in mm) of the Earth have to be in order for the escape speed of the Earth to equal (1/21) times the speed of light (300000000 m/s)? You may ignore all other gravitational interactions for the rocket and assume that the Earth-rocket system is isolated. Hint: the mass of the Earth is 5.94 x 1024kg and G=6.67×10−11Jmkg2G=6.67\times10^{-11}\frac{Jm}{kg^2}G=6.67×10−11kg2Jm​

in progress 0
Orla Orla 3 years 2021-07-16T01:33:44+00:00 1 Answers 77 views 0

Answers ( )

  1. trungdung22
    0
    2021-07-16T01:35:35+00:00
    Reply

    Answer:

    The expected radius of the Earth is 3.883 meters.

    Explanation:

    The formula for the escape speed is derived from Principle of Energy Conservation and knowing that rocket is initially at rest on the surface of the Earth and final energy is entirely translational kinetic, that is:

    U = K (1)

    Where:

    U – Gravitational potential energy, in joules.

    K – Translational kinetic energy, in joules.

    Then, we expand the formula by definitions of potential and kinetic energy:

    \frac{G\cdot M\cdot m}{r} = \frac{1}{2}\cdot m \cdot v^{2} (2)

    Where:

    G – Gravitational constant, in cubic meters per kilogram-square second.

    M – Mass of the Earth. in kilograms.

    m – Mass of the rocket, in kilograms.

    r – Radius of the Earth, in meters.

    v – Escape velocity, in meters per second.

    Then, we derive an expression for the escape velocity by clearing it within (2):

    \frac{GM}{r} = \frac{1}{2}\cdot v^{2}

    v = \sqrt{\frac{2\cdot G \cdot M}{r} } (3)

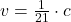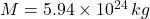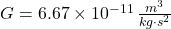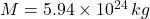    If we know that v = \frac{1}{21}\cdot c, c = 3\times 10^{8}\,\frac{m}{s}, M = 5.94\times 10^{24}\,kg, G = 6.67\times 10^{-11}\,\frac{m^{3}}{kg\cdot s^{2}} and M = 5.94\times 10^{24}\,kg, then the expected radius of the Earth is:

    \frac{GM}{r} = \frac{1}{2}\cdot v^{2}

    r = \frac{2\cdot G \cdot M}{v^{2}}

    r = \frac{2\cdot \left(6.67\times 10^{-11}\,\frac{m^{3}}{kg\cdot s^{2}} \right)\cdot (5.94\times 10^{24}\,kg)}{\left[\frac{1}{21}\cdot \left(3\times 10^{8}\,\frac{m}{s} \right) \right]^{2}}

    r = 3.883\,m

    The expected radius of the Earth is 3.883 meters.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )