Share
write a coordinate proof. Given: Rectangle ABCD has vertices A(0,4), B(6,4), C(6,0), D(0,0). E is the midpoint of line DC. F is the midpoint
Question
write a coordinate proof. Given: Rectangle ABCD has vertices A(0,4), B(6,4), C(6,0), D(0,0). E is the midpoint of line DC. F is the midpoint of line DA. Prove: The area of rectangle DEGF is one fourth the area of rectangle ABCD.
Please help I’ve been trying for a while
in progress
0
Mathematics
4 years
2021-08-14T19:05:47+00:00
2021-08-14T19:05:47+00:00 1 Answers
81 views
0

Answers ( )
Answer:
The answer is below
Step-by-step explanation:
Distance between two points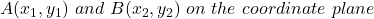
The area of rectangle = length * breadth
The area of rectangle ABCD = |AB| * |BC|
The area of rectangle ABCD = |AB| * |BC| = 6 * 4 = 24
E(x, y) is midpoint of line DC. Its coordinate is:
x = (6 + 0) / 2 = 3; y = (0 + 0) / 2 =0
The coordinate of E = (3, 0)
F(a, b) is midpoint of line DA. Its coordinate is:
a = (0 + 0) / 2 = 0; b = (4 + 0) / 2 = 2
The coordinate of E = (0, 2)
The area of rectangle DEGF = |DE| * |DF|
The area of rectangle ABCD = |DE| * |DF| = 3 * 2 = 6
Therefore, area of rectangle DEGF is one fourth the area of rectangle ABCD