write the following expression in the form (x+a)^2+b a)x^2+6x+4​

Question

write the following expression in the form (x+a)^2+b

a)x^2+6x+4​

in progress 0
Xavia 4 years 2021-08-04T13:30:25+00:00 1 Answers 16 views 0

Answers ( )

  1. Jezebel
    0
    2021-08-04T13:32:13+00:00
    Reply

    Answer:

    The given expression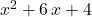 x^2 + 6\, x + 4 is equivalent to 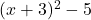(x + 3)^2 - 5. In this expression, a = 3 whereas b = -5.

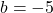    Step-by-step explanation:

    Expand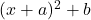 (x + a)^2 + b using binomial expansion.

    \begin{aligned} & (x + a)^2 + b \\ &= (x + a) \cdot (x + a) + b \\ &= \left(x^2 + a\, x\right) + \left(a\, x + a^2\right) + b \\ &= x^2 + 2\, a\, x + (a^2 + b)\end{aligned}.

    Compare this expression to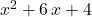 x^2 + 6\, x + 4 to find information about a and b.

    In particular, these two expressions are supposed to be equal to one another. Therefore:

    • The coefficient of the x^2 term in these two expressions should be the same. The coefficient of x^2\! in both expression is 1. That does not provide any information about a or about b.
    • The coefficient of the x term in these two expressions should be the same. In the first equation, the coefficient of x\! is 2\, a. In the second equation, that coefficient is 6. Therefore, 2\, a = 6.
    • The constant term of these two expressions should be the same. That gives the equation: a^2 + b = 4.

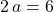    The first equation 2\, a = 6 implies that a = 3. Substitute that value into the second equation and solve for b. The conclusion is that 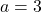a= 3 and b = -5.

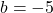    Therefore, the original equation is equivalent to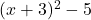 (x + 3)^2 - 5.

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )