4. Write an equation for the line that is parallel to the given line and that passes through the given point. y = 5/2x-10;(-6,-2

Question

4. Write an equation for the line that is parallel to the given line and that passes
through the given point.
y = 5/2x-10;(-6,-29)

in progress 0
Diễm Kiều 4 years 2021-08-24T03:31:52+00:00 1 Answers 42 views 0

Answers ( )

  1. Gerda
    0
    2021-08-24T03:33:25+00:00
    Reply

    Answer:

    y=\frac{5}{2}x-14

    Step-by-step explanation:

    Hi there!

    What we need to know:

    • Linear equations are typically organized in slope-intercept form: y=mx+b where m is the slope and b is the y-intercept (the value of y when x is 0)
    • Parallel lines always have the same slope

    1) Determine the slope (m)

    y=\frac{5}{2}x-10

    In the given equation, \frac{5}{2} is in the place of m, making it the slope. Because parallel lines have the same slope, the line we’re currently solving for therefore has a slope of \frac{5}{2}. Plug this into y=mx+b:

    y=\frac{5}{2}x+b

    2) Determine the y-intercept (b)

    y=\frac{5}{2}x+b

    Plug in the given point (-6,-29) and solve for b

    -29=\frac{5}{2}(-6)+b

    Simplify -6 and 2

    -29=\frac{5}{1}(-3)+b\\-29=(5)}(-3)+b\\-29=-15+b

    Add 15 to both sides to isolate b

    -29+15=-15+b+15\\-14=b

    Therefore, the y-intercept is -14. Plug this back into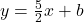 y=\frac{5}{2}x+b:

    y=\frac{5}{2}x-14

    I hope this helps!

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )