Share
4. An angle is 50° more than its supplement. Find the angles.
Question
4. An angle is 50° more than its supplement. Find the angles.
in progress
0
Mathematics
4 years
2021-08-23T02:31:40+00:00
2021-08-23T02:31:40+00:00 1 Answers
15 views
0

Answers ( )
Answer:
The angles measure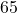 ° and
° and 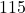 °.
°.
Step-by-step explanation:
Supplementary angles are a pair of angles whose measures add up to °. In this case, we know that one angle is
°. In this case, we know that one angle is  ° bigger than the other one, so if we let the measure of one angle be
° bigger than the other one, so if we let the measure of one angle be  , then the measure of the other angle will be
, then the measure of the other angle will be 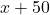 . Therefore, we can write the following equation to solve for
. Therefore, we can write the following equation to solve for
Solving for , we get:
, we get:
Therefore,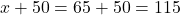 , so our final answer is that the angles measure
, so our final answer is that the angles measure 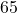 ° and
° and 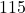 °. Hope this helps!
°. Hope this helps!