Share
26.- Un cable de luz del # 10 mide 88 metros de longitud y 26 cm de diámetro se estira por medio de una fuerza de 380 N Calcular: (a)
Question
26.- Un cable de luz del # 10 mide 88 metros de longitud y 26 cm de diámetro se estira por medio de una fuerza de 380 N Calcular:
(a) ¿Cuál es el esfuerzo longitudinal? Si la longitud después del alargamiento es de 88.10 metros,
(b) ¿Cuál es su deformación longitudinal?
(c) Determine el módulo de Young para el alambre.
E =7169.81N / m2
in progress
0
Physics
4 years
2021-08-06T23:34:29+00:00
2021-08-06T23:34:29+00:00 1 Answers
77 views
0

Answers ( )
Answer:
(a) El esfuerzo longitudinal es 7169.811 newtons por metro cuadrado, (b) Hay una deformación longitudinal absoluta de 0.10 metros y una deformación longitudinal unitaria de 1.136 × 10⁻³, (c) El módulo de Young es 6,311,453.345 newtons por metro cuadrado.
Explanation:
(a) El esfuerzo longitudinal ( ) del cable, medido en newtons por metro cuadrado, es determinada por la siguiente expresión:
) del cable, medido en newtons por metro cuadrado, es determinada por la siguiente expresión:
Donde:
Asimismo, el área transversal del cable de determina mediante esta fórmula:
Donde:
Si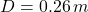 y
y 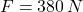 , entonces:
, entonces:
El esfuerzo longitudinal es 7169.811 newtons por metro cuadrado.
(b) La deformación longitudinal unitaria ( ), adimensional, se determina con esta fórmula:
), adimensional, se determina con esta fórmula:
Donde:
Dado que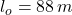 y
y 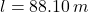 , la deformación longitudinal unitaria es:
, la deformación longitudinal unitaria es:
Hay una deformación longitudinal absoluta de 0.10 metros y una deformación longitudinal unitaria de 1.136 × 10⁻³.
(c) El módulo de Young ( ), medido en newtons por metro cuadrado, es definido por la siguiente relación:
), medido en newtons por metro cuadrado, es definido por la siguiente relación:
Si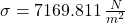 y
y 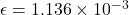 , entonces:
, entonces:
El módulo de Young es 6,311,453.345 newtons por metro cuadrado.