Share
20. Give an example of a function from N to N that is a) one-to-one but not onto. b) onto but not one-to-one. c) both onto and one-to-one (b
Question
20. Give an example of a function from N to N that is a) one-to-one but not onto. b) onto but not one-to-one. c) both onto and one-to-one (but different from the identity function). d) neither one-to-one nor onto.
in progress
0
Mathematics
4 years
2021-08-16T10:44:14+00:00
2021-08-16T10:44:14+00:00 1 Answers
1122 views
0

Answers ( )
Answer:
Step-by-step explanation:
a) To provide an example of a function N → N that is one-to-one but not onto.
Suppose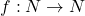 to be
to be 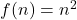
Then;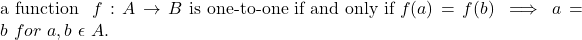
Now, assuming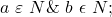
Then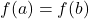
The above function is said to be one-to-one
2 is not a perfect square, hence, it is not regarded as the image of any natural no.
As such, f is not onto.
We can thereby conclude that the function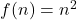 is one-to-one but not onto
is one-to-one but not onto
b)
It implies that the function is not one-to-one since there exist different natural no. having the same image.
So, for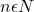 , there exists an image of 2n in N
, there exists an image of 2n in N
i.e.
Hence, the function is onto
We thereby conclude that the function![Rendered by QuickLaTeX.com f(n) = [n/2] \text{ is onto but not one-to-one}](https://documen.tv/wp-content/ql-cache/quicklatex.com-2e79e77523ac77180b3d7f639b13bad8_l3.png)
c)
So, if n, m is odd:
Then:
Likewise, if n, m is even:
Then;
The function is then said to be one-to-one.
However, For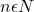 and is odd, there exists an image of
and is odd, there exists an image of  that is even;
that is even;
For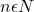 and is even, there exists an image of
and is even, there exists an image of 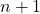 that is odd;
that is odd;
where(; implies such that)
Hence, this function is said to be onto.
We can therefore conclude that the function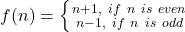 is both onto and one-to-one.
is both onto and one-to-one.
d)
Here, to provide an example where the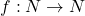 is neither one-to-one nor onto.
is neither one-to-one nor onto.
SO;
Let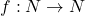 is defined to be
is defined to be 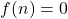
Then, since every integer has the same image as zero(0), the function is not one-to-one.
Similarly, the function is not onto since every positive integer is not an image of any natural number.
We, therefore conclude that, the function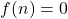 is neither one-to-one nor onto.
is neither one-to-one nor onto.