Share
find the magnitude of u cross v and the unit vector parallel to u cross v in the direction of u cross v u=2i+2j-k, v=-i+k
Question
Lost your password? Please enter your email address. You will receive a link and will create a new password via email.
Answers ( )
Recall that
where is the angle between the vectors
is the angle between the vectors 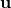 and
and 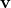 . No need to actually compute the cross product.
. No need to actually compute the cross product.
We can find the angle between the vectors using the dot product formula,
Then