A stone is tossed horizontally from the highest point of a 95 m building and lands 105 m from the base of the building. Ignore air resistanc

Question

A stone is tossed horizontally from the highest point of a 95 m building and lands 105 m from the base of the building. Ignore air resistance, and use a coordinate system whose origin is at the highest point of the building, with positive y upwards and positive x in the direction of the throw.
A. How long is the stone in the air in s?
B. What must have been the initial horizontal component of the velocity, in m/s?
C. What is the vertical component of the velocity just before the stone hits the ground, in m/s?
D. What is the magnitude of the velocity of the stone just before it hits the ground, in m/s?

in progress 0
Linh Đan 4 years 2021-07-19T15:27:18+00:00 1 Answers 28 views 0

Answers ( )

  1. Nick
    0
    2021-07-19T15:29:16+00:00
    Reply

    Answer:

    A) t = 4.40 s
    , B)   v = 23.86 m / s
    ,  c)  v_y = – 43.12 m / s
    , D)  v = 49.28 m/s

    Explanation:

    This is a projectile throwing exercise,

    A) To know the time of the stone in the air, let’s find the time it takes to reach the floor

              y = y₀ +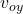 v_{oy} t – ½ g t²

    as the stone is thrown horizontally  v_{oy} = 0

              y = y₀ – ½ g t²

              0 = y₀ – ½ g t²

              t = √ (2 y₀ / g)

              t = √ (2 95 / 9.8)

              t = 4.40 s

    B) what is the horizontal velocity of the body

              v = x / t

              v = 105 / 4.40

              v = 23.86 m / s

    C) The vertical speed when it touches the ground

              v_y =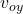 v_{oy} – g t

              v_y = 0 – 9.8 4.40

              v_y = – 43.12 m / s

    the negative sign indicates that the speed is down

    D) total velocity just hitting the ground

              v = vₓ i ^ + v_y j ^

              v = 23.86 i ^ – 43.12 j ^

    Let’s use Pythagoras’ theorem to find the modulus

              v = √ (vₓ² + v_y²)

              v = √ (23.86² + 43.12²)

               v = 49.28 m / s

    we use trigonometry for the angle

              tan θ = v_y / vₓ

              θ = tan⁻¹ (-43.12 / 23.86)

               
    θ = -61

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )