A spherical shell rolls without sliding along the floor. The ratio of its rotational kinetic energy (about an axis through its center of mas

Question

A spherical shell rolls without sliding along the floor. The ratio of its rotational kinetic energy (about an axis through its center of mass) to its translational kinetic energy is:

in progress 0
Huyền Thanh 4 years 2021-08-20T09:53:46+00:00 1 Answers 11 views 0

Answers ( )

  1. quangkhai
    0
    2021-08-20T09:54:59+00:00
    Reply

    Answer:

    The ratio  is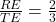  \frac{RE}{TE} = \frac{2}{3}

    Explanation:

    Generally  the Moment of inertia of a spherical object (shell) is mathematically represented as

                  I = \frac{2}{3} * m r^2

    Where m is  the mass of the spherical object

           and   r is the radius  

    Now the the rotational kinetic energy can be mathematically represented as

           RE = \frac{1}{2}* I * w^2

    Where  w is the angular velocity which is mathematically represented as

                 w = \frac{v}{r}

    =>           w^2 = [\frac{v}{r}] ^2

    So

                 RE = \frac{1}{2}* [\frac{2}{3} *mr^2] * [\frac{v}{r} ]^2

                RE = \frac{1}{3} * mv^2

    Generally the transnational  kinetic energy of this motion is  mathematically represented as

                    TE = \frac{1}{2} mv^2

    So  

          \frac{RE}{TE} = \frac{\frac{1}{3} * mv^2}{\frac{1}{2} * m*v^2}

           \frac{RE}{TE} = \frac{2}{3}

Leave an answer

Browse

Giải phương trình 1 ẩn: x + 2 - 2(x + 1) = -x . Hỏi x = ? ( )