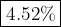Share
A 4 cm diameter “bobber” with a mass of 3 grams floats on a pond. A thin, light fishing line is tied to the bottom of the bobber, and from t
Question
A 4 cm diameter “bobber” with a mass of 3 grams floats on a pond. A thin, light fishing line is tied to the bottom of the bobber, and from the bottom hangs a 10 gram lead weight. The density of lead is 11.3 g/cm3. What fraction of the bobber’s volume is submerged, as a percent of the total volume
in progress
0
Physics
4 years
2021-08-26T20:52:24+00:00
2021-08-26T20:52:24+00:00 1 Answers
92 views
0

Answers ( )
Answer:
Explanation:
Calculate the volume of the lead
Now calculate the bouyant force acting on the lead
This force will act in upward direction
Gravitational force on the lead due to its mass will act in downward direction
Hence the difference of this two force
If V is the volume submerged in the water then bouyant force on the bobber is
Equate bouyant force with the tension and gravitational force
Now Total volume of bobble is
=